Neil Yorke-Smith
Deep Learning--Accelerated Multi-Start Large Neighborhood Search for Real-time Freight Bundling
Dec 12, 2025



Abstract:Online Freight Exchange Systems (OFEX) play a crucial role in modern freight logistics by facilitating real-time matching between shippers and carrier. However, efficient combinatorial bundling of transporation jobs remains a bottleneck. We model the OFEX combinatorial bundling problem as a multi-commodity one-to-one pickup-and-delivery selective traveling salesperson problem (m1-PDSTSP), which optimizes revenue-driven freight bundling under capacity, precedence, and route-length constraints. The key challenge is to couple combinatorial bundle selection with pickup-and-delivery routing under sub-second latency. We propose a learning--accelerated hybrid search pipeline that pairs a Transformer Neural Network-based constructive policy with an innovative Multi-Start Large Neighborhood Search (MSLNS) metaheuristic within a rolling-horizon scheme in which the platform repeatedly freezes the current marketplace into a static snapshot and solves it under a short time budget. This pairing leverages the low-latency, high-quality inference of the learning-based constructor alongside the robustness of improvement search; the multi-start design and plausible seeds help LNS to explore the solution space more efficiently. Across benchmarks, our method outperforms state-of-the-art neural combinatorial optimization and metaheuristic baselines in solution quality with comparable time, achieving an optimality gap of less than 2\% in total revenue relative to the best available exact baseline method. To our knowledge, this is the first work to establish that a Deep Neural Network-based constructor can reliably provide high-quality seeds for (multi-start) improvement heuristics, with applicability beyond the \textit{m1-PDSTSP} to a broad class of selective traveling salesperson problems and pickup and delivery problems.
Sufficient Decision Proxies for Decision-Focused Learning
May 06, 2025Abstract:When solving optimization problems under uncertainty with contextual data, utilizing machine learning to predict the uncertain parameters is a popular and effective approach. Decision-focused learning (DFL) aims at learning a predictive model such that decision quality, instead of prediction accuracy, is maximized. Common practice here is to predict a single value for each uncertain parameter, implicitly assuming that there exists a (single-scenario) deterministic problem approximation (proxy) that is sufficient to obtain an optimal decision. Other work assumes the opposite, where the underlying distribution needs to be estimated. However, little is known about when either choice is valid. This paper investigates for the first time problem properties that justify using either assumption. Using this, we present effective decision proxies for DFL, with very limited compromise on the complexity of the learning task. We show the effectiveness of presented approaches in experiments on problems with continuous and discrete variables, as well as uncertainty in the objective function and in the constraints.
Epistemic Wrapping for Uncertainty Quantification
May 04, 2025Abstract:Uncertainty estimation is pivotal in machine learning, especially for classification tasks, as it improves the robustness and reliability of models. We introduce a novel `Epistemic Wrapping' methodology aimed at improving uncertainty estimation in classification. Our approach uses Bayesian Neural Networks (BNNs) as a baseline and transforms their outputs into belief function posteriors, effectively capturing epistemic uncertainty and offering an efficient and general methodology for uncertainty quantification. Comprehensive experiments employing a Bayesian Neural Network (BNN) baseline and an Interval Neural Network for inference on the MNIST, Fashion-MNIST, CIFAR-10 and CIFAR-100 datasets demonstrate that our Epistemic Wrapper significantly enhances generalisation and uncertainty quantification.
Generalized Decision Focused Learning under Imprecise Uncertainty--Theoretical Study
Feb 25, 2025Abstract:Decision Focused Learning has emerged as a critical paradigm for integrating machine learning with downstream optimisation. Despite its promise, existing methodologies predominantly rely on probabilistic models and focus narrowly on task objectives, overlooking the nuanced challenges posed by epistemic uncertainty, non-probabilistic modelling approaches, and the integration of uncertainty into optimisation constraints. This paper bridges these gaps by introducing innovative frameworks: (i) a non-probabilistic lens for epistemic uncertainty representation, leveraging intervals (the least informative uncertainty model), Contamination (hybrid model), and probability boxes (the most informative uncertainty model); (ii) methodologies to incorporate uncertainty into constraints, expanding Decision-Focused Learning's utility in constrained environments; (iii) the adoption of Imprecise Decision Theory for ambiguity-rich decision-making contexts; and (iv) strategies for addressing sparse data challenges. Empirical evaluations on benchmark optimisation problems demonstrate the efficacy of these approaches in improving decision quality and robustness and dealing with said gaps.
Learning optimal objective values for MILP
Nov 27, 2024



Abstract:Modern Mixed Integer Linear Programming (MILP) solvers use the Branch-and-Bound algorithm together with a plethora of auxiliary components that speed up the search. In recent years, there has been an explosive development in the use of machine learning for enhancing and supporting these algorithmic components. Within this line, we propose a methodology for predicting the optimal objective value, or, equivalently, predicting if the current incumbent is optimal. For this task, we introduce a predictor based on a graph neural network (GNN) architecture, together with a set of dynamic features. Experimental results on diverse benchmarks demonstrate the efficacy of our approach, achieving high accuracy in the prediction task and outperforming existing methods. These findings suggest new opportunities for integrating ML-driven predictions into MILP solvers, enabling smarter decision-making and improved performance.
Machine Learning Augmented Branch and Bound for Mixed Integer Linear Programming
Feb 08, 2024



Abstract:Mixed Integer Linear Programming (MILP) is a pillar of mathematical optimization that offers a powerful modeling language for a wide range of applications. During the past decades, enormous algorithmic progress has been made in solving MILPs, and many commercial and academic software packages exist. Nevertheless, the availability of data, both from problem instances and from solvers, and the desire to solve new problems and larger (real-life) instances, trigger the need for continuing algorithmic development. MILP solvers use branch and bound as their main component. In recent years, there has been an explosive development in the use of machine learning algorithms for enhancing all main tasks involved in the branch-and-bound algorithm, such as primal heuristics, branching, cutting planes, node selection and solver configuration decisions. This paper presents a survey of such approaches, addressing the vision of integration of machine learning and mathematical optimization as complementary technologies, and how this integration can benefit MILP solving. In particular, we give detailed attention to machine learning algorithms that automatically optimize some metric of branch-and-bound efficiency. We also address how to represent MILPs in the context of applying learning algorithms, MILP benchmarks and software.
Mixed-Integer Optimisation of Graph Neural Networks for Computer-Aided Molecular Design
Dec 02, 2023Abstract:ReLU neural networks have been modelled as constraints in mixed integer linear programming (MILP), enabling surrogate-based optimisation in various domains and efficient solution of machine learning certification problems. However, previous works are mostly limited to MLPs. Graph neural networks (GNNs) can learn from non-euclidean data structures such as molecular structures efficiently and are thus highly relevant to computer-aided molecular design (CAMD). We propose a bilinear formulation for ReLU Graph Convolutional Neural Networks and a MILP formulation for ReLU GraphSAGE models. These formulations enable solving optimisation problems with trained GNNs embedded to global optimality. We apply our optimization approach to an illustrative CAMD case study where the formulations of the trained GNNs are used to design molecules with optimal boiling points.
Robust Losses for Decision-Focused Learning
Oct 06, 2023



Abstract:Optimization models used to make discrete decisions often contain uncertain parameters that are context-dependent and are estimated through prediction. To account for the quality of the decision made based on the prediction, decision-focused learning (end-to-end predict-then-optimize) aims at training the predictive model to minimize regret, i.e., the loss incurred by making a suboptimal decision. Despite the challenge of this loss function being possibly non-convex and in general non-differentiable, effective gradient-based learning approaches have been proposed to minimize the expected loss, using the empirical loss as a surrogate. However, empirical regret can be an ineffective surrogate because the uncertainty in the optimization model makes the empirical regret unequal to the expected regret in expectation. To illustrate the impact of this inequality, we evaluate the effect of aleatoric and epistemic uncertainty on the accuracy of empirical regret as a surrogate. Next, we propose three robust loss functions that more closely approximate expected regret. Experimental results show that training two state-of-the-art decision-focused learning approaches using robust regret losses improves test-sample empirical regret in general while keeping computational time equivalent relative to the number of training epochs.
Learning to branch with Tree MDPs
May 31, 2022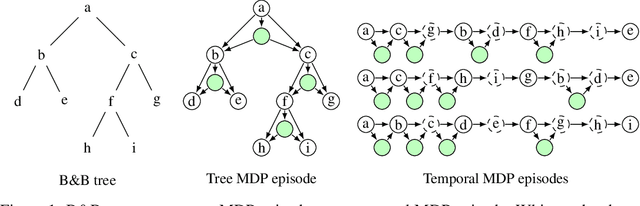
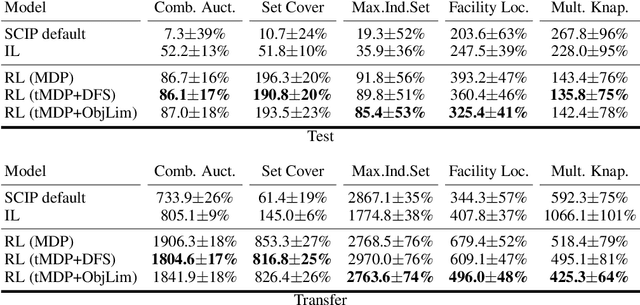
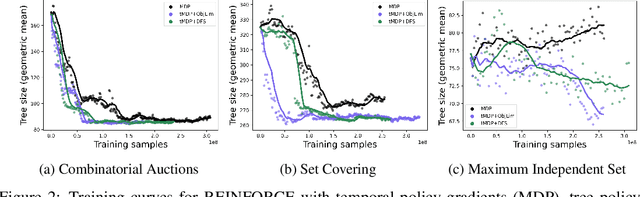
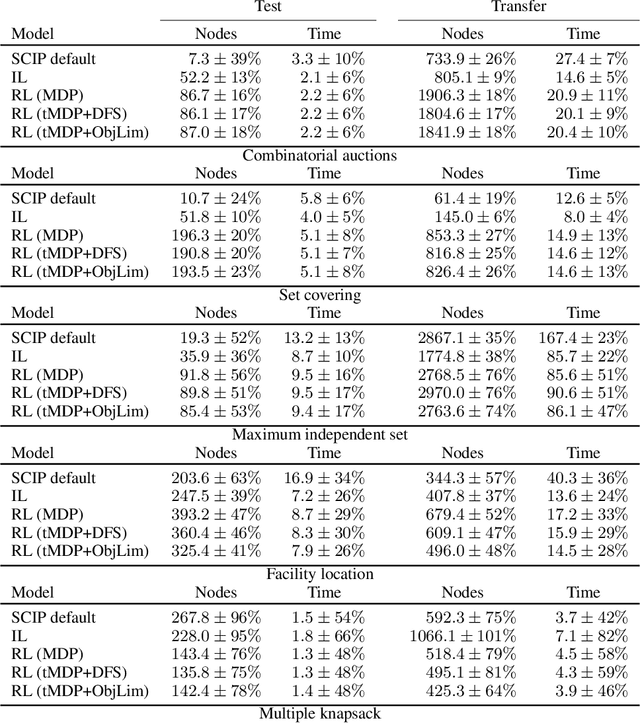
Abstract:State-of-the-art Mixed Integer Linear Program (MILP) solvers combine systematic tree search with a plethora of hard-coded heuristics, such as the branching rule. The idea of learning branching rules from data has received increasing attention recently, and promising results have been obtained by learning fast approximations of the strong branching expert. In this work, we instead propose to learn branching rules from scratch via Reinforcement Learning (RL). We revisit the work of Etheve et al. (2020) and propose tree Markov Decision Processes, or tree MDPs, a generalization of temporal MDPs that provides a more suitable framework for learning to branch. We derive a tree policy gradient theorem, which exhibits a better credit assignment compared to its temporal counterpart. We demonstrate through computational experiments that tree MDPs improve the learning convergence, and offer a promising framework for tackling the learning-to-branch problem in MILPs.
Machine Learning for Combinatorial Optimisation of Partially-Specified Problems: Regret Minimisation as a Unifying Lens
May 20, 2022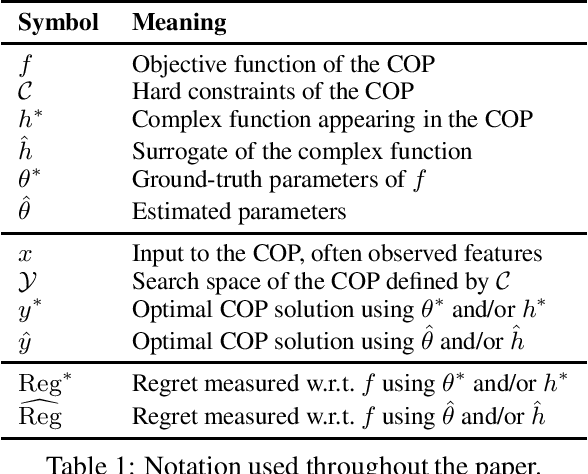

Abstract:It is increasingly common to solve combinatorial optimisation problems that are partially-specified. We survey the case where the objective function or the relations between variables are not known or are only partially specified. The challenge is to learn them from available data, while taking into account a set of hard constraints that a solution must satisfy, and that solving the optimisation problem (esp. during learning) is computationally very demanding. This paper overviews four seemingly unrelated approaches, that can each be viewed as learning the objective function of a hard combinatorial optimisation problem: 1) surrogate-based optimisation, 2) empirical model learning, 3) decision-focused learning (`predict + optimise'), and 4) structured-output prediction. We formalise each learning paradigm, at first in the ways commonly found in the literature, and then bring the formalisations together in a compatible way using regret. We discuss the differences and interactions between these frameworks, highlight the opportunities for cross-fertilization and survey open directions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge